1. Oldal
Kepler második törvénye:
Kepler második törvénye, más néven a területegyenlőség törvénye, kimondja, hogy a Napot egy bolygóval összekötő vezérsugár egyenlő időközök alatt egyenlő területeket súrol . Ez azt jelenti, hogy a bolygó legtávolabbi pontján (aféliumban) a leglassabban, legközelebbi pontján (perihéliumban) pedig a leggyorsabban halad . A törvény az impulzusnyomaték-megmaradás következménye az égitestek pályamozgásában, és megmagyarázza, hogyan változik a bolygó sebessége azért, hogy a súrolt terület sebessége állandó maradjon .
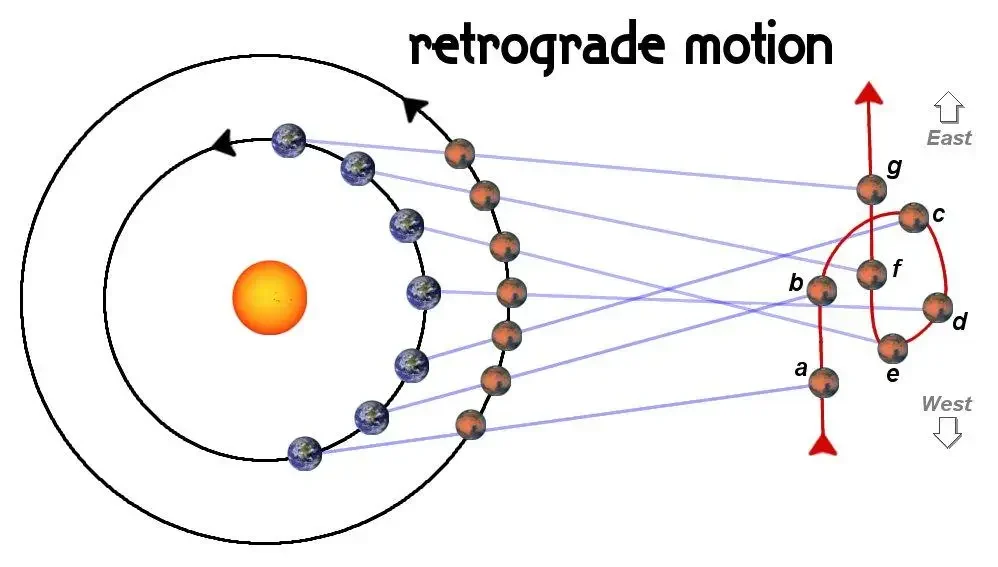
A Mars retrográd mozgása: Földi perspektívából származó illúzió:
A Mars retrográd mozgása a Mars látszólagos hátramozdulása az égbolton, amely akkor figyelhető meg, amikor a Föld megelőzi a Marsot a Nap körüli pályájukon. Ez annak köszönhető, hogy a Föld rövidebb keringési ideje (365 nap) miatt gyorsabban mozog, mint a Mars (687 napos keringés), és ezzel optikai csalást kelt: a Mars irányt változtatni látszik a távoli csillagok háttérében. A jelenség 780 naponként (szinódikus periódus) ismétlődik, és történelmileg a heliocentrikus modell segítségével oldották meg, amely megerősítette, hogy a bolygók a Nap, és nem a Föld körül keringenek.
Inercia rendszerek viszonya:
Az inerciális vonatkoztatási rendszerekben a testek megőrzik nyugalmi vagy egyenes vonalú egyenletes mozgásukat, amíg erő hatásra nem kerülnek (Newton első törvénye). Ezen animációban egy vízszintes mozgással pattogó labda cikcakkos pályát követ, amikor egy álló vonatkoztatási rendszerből (pl. a földön álló kamera) figyeljük. Ugyanakkor a labdához rögzített inerciális rendszerből (amely állandó sebességgel mozog a földhöz képest) a labda csak függőlegesen mozog, míg a talaj és a kamera horizontálisan halad el alatta. Ez jól szemlélteti a mozgás relativitását: a mozgás leírása a megfigyelő rendszerétől függ, de a fizikai törvények minden inerciális rendszerben ugyanazok.
A Rugóerő Eloszlása Különböző Elrendezésekben:
A rugók Hooke törvénye szerint viselkednek (F=DΔx), ahol az erő arányos a megnyúlással. Soros elrendezésben a rugókat ugyanaz az erő terheli, ami lágyabb eredő rugóállandót eredményez (1/Deq=1/D1+1/D2). Párhuzamos elrendezésben a terhelés megosztik a rugók között, ami merevebb rendszert hoz létre (Deq=D1+D2). Ezek az elvek határozzák meg, hogyan oszlik el az erő a fizikai rendszerekben lévő rugókban, befolyásolva azok eredő merevségét és megnyúlását a terhelés hatására.
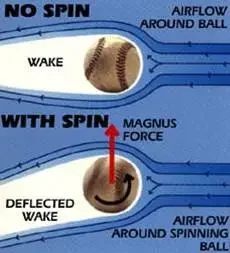
Miért kanyarodnak el a pörgő labdák:
A Magnus-effektus egy fizikai jelenség, amely során egy pörgő tárgy (például egy labda) oldalirányú erő hatására megy keresztül, merőlegesen a mozgásiránya és a pörgési tengelye síkjára . Ahogy a labda pörög, maga után húzza a környező levegőmolekulákat, nyomáskülönbséget hozva létre az ellentétes oldalai között – magasabb nyomás az egyik, alacsonyabb nyomás a másik oldalon . Ez a nyomáskülönbség egy nettó erőt (Magnus-erő) hoz létre, amely miatt a labda pályája jelentősen elgörbül . A jelenséget matematikailag az FM⃗=S(ω⃗×v⃗) egyenlet írja le, ahol az erő a pörgési vektortól és a sebességtől függ . Ennek az elvnek a megértése alapvető olyan sportágakban, mint a labdarúgás, vagy a fluidumdinamikát érintő fizikai alkalmazásokban .
Hogyan működik valójában a szívószál? A légnyomás ereje:
Amikor szívószállal iszol, a tüdőd kitágul, csökkentve a légnyomást a szívószál belsejében. A szívószálon kívüli folyadékfelszínt érő magasabb légnyomás ezután felfelé nyomja a folyadékot, hogy kiegyenlítse ezt a nyomáskülönbséget. Ez azt mutatja, hogy a folyadékáramlást a légnyomás hajtja, és nem valamilyen “szívóerő”. A folyadék emelkedésének maximális magasságát a légnyomás korlátozza (víz esetében kb. 10,3 méter). Így a szívószálak alapvető nyomáselvén működnek, nem vákuumos szívásen.
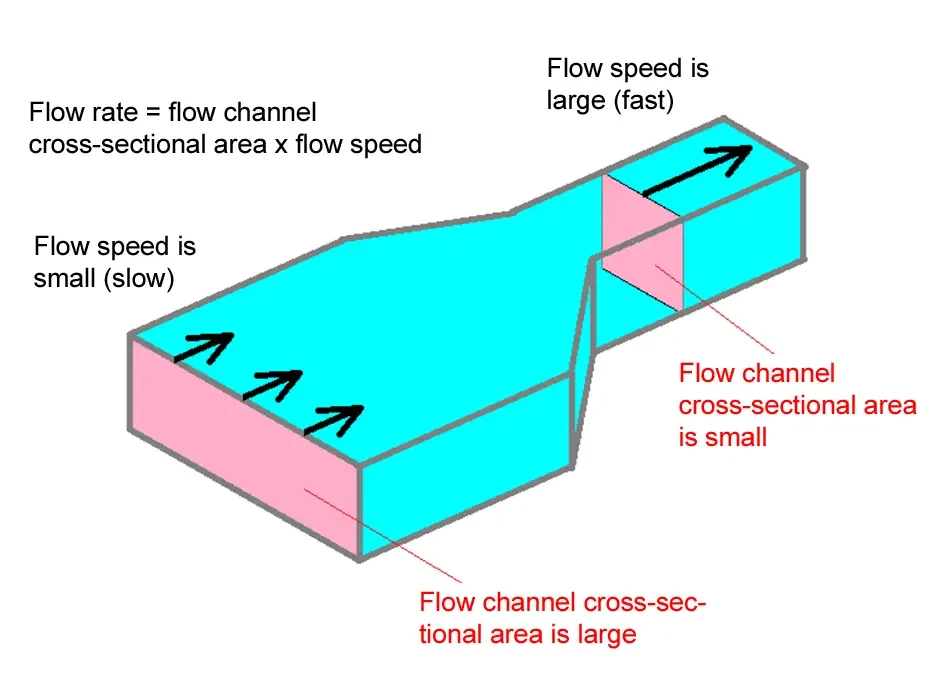
Folyamáramlás dinamikája: Miért gyorsabb a szűkebb szakaszon:
A tömegmegmaradás elve a folyadékdinamikában azt mondja ki, hogy egy folyó vízhozama állandó. Amikor a folyó szűkül, a keresztmetszeti terület csökken, ami miatt a víznek gyorsabban kell áramlania ugyanazon vízmennyiség fenntartása érdekében. Ezt az elvet szaggatott vonalak (áramvonalak) és pontok mozgása szemlélteti: a pontok lassabban haladnak a szélesebb szakaszokon, és gyorsabban a szűkebb részeken. Az animáció azt mutatja be, hogy a sebesség hogyan fordítottan arányos a csatorna szélességével. Ennek az elvnek a megértése segít megmagyarázni olyan természeti jelenségeket, mint az erózió mintázata vagy az árvízi viselkedés.
A súlytalanság megértése: A keringés fizikája:
Az asztronauták nem azért tapasztalnak súlytalanságot, mert a gravitáció hiányzna – valójában a Föld gravitációja a Nemzetközi Űrállomás magasságában is még a felszíni érték mintegy 90%-a. Ehelyett a súlytalanság azért következik be, mert maga az űrjármű és a benne lévő személyek egyaránt folyamatos szabadeséssel, szabadon esnek a Föld körül. A gravitáció vonzza az űrállomást a Föld középpontja felé, míg a tangenciális sebesség előre mozgatja. Ezek az erők összeadódnak, stabil pályát hozva létre, ahol minden együtt és egyforma gyorsulással mozog. Ez megszünteti a relatív mozgást, és kelti a súlytalanság érzetét. Ez egy olyan állandó szabadesés állapota, ahol nincs támasztó erő, és a gravitációs vonzás és a keringési mozgás tökéletes egyensúlyban van.
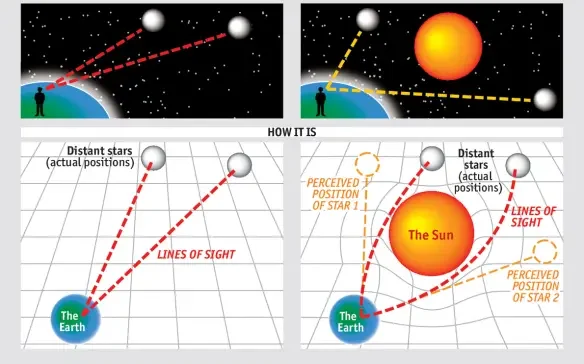
Eddington 1919-es napfogyatkozási kísérlete: Einstein elméletének bizonyítéka:
Ez az animáció bemutatja Arthur Eddington 1919-es, történelmi jelentőségű kísérletét, amelyben a csillagfény látszólagos eltérését mérte egy napfogyatkozás alkalmával. Az elhajlás abból adódott, hogy a Nap tömege meghajlítja a téridőt, és ezzel eltéríti a távoli csillagokból érkező fénysugarakat. Eddington csapata összehasonlította a fogyatkozás alatt készült felvételeket a referencia-éjszakai égbolttal, felfedve a csillagok helyzetének mérhető, kifelé irányuló eltolódását. A megfigyelt eltérés megegyezett Einstein 1,75 ívmásodperces előrejelzésével, megerősítve az általános relativitáselméletet és forradalmasítva a gravitációról alkotott képünket. Ez a kísérlet szolgáltatott az első közvetlen bizonyítékot arra, hogy a gravitáció meghajlítja a fényt.
Miért melegszik fel a kerékpárpumpa? A kompressziós munka fizikája:
Amikor gyorsan összenyomjuk a levegőt egy kerékpárpumpában, a gázon végzett munka növeli annak belső energiáját, ahogyan azt a termodinamika első főtétele írja le (ΔU=Q−W). Ez az adiabatikus folyamat nem hagy időt a hőcserére a környezettel, így a befektetett munka közvetlenül hőenergiává alakul. Mikroszkópikus szinten a molekulák kinetikus energiája nő és gyakoribbak az ütközések, ami emeli a hőmérsékletet. A pumpa dugattyúja és hengere ennek az energiaátadásnak az eredményeként melegedik fel, jól szemléltetve, hogyan alakul át a mechanikai munka hőenergiává.
Miért súlyosabbabb a gőz okozta égés, mint a forró vízé:
A 100°C-os gőz súlyosabb égést okoz, mint az azonos hőmérsékletű forró víz, mert sokkal több energiát ad le a bőrrel való érintkezéskor. A gőz lecsapódáskor először nagymennyiségű lágyulási hőt (2257 J/g) szabadít fel, ami a víz gőzzé alakulása során felvett energia. Ezt követi a érzékelhető hő leadása, amikor a lecsapódott víz lehűl a bőr hőmérsékletére (≈264 J/g). Ezzel szemben a forró víz csak érzékelhető hőt ad le (≈264 J/g). A gőz összesen kb. 9,5-szer több energiát visz át mint a forró víz, ami gyorsabb hőátadással és mélyebb szöveti károsodással jár.
A hűtőszekrény és a termodinamika második főtétele:
A hűtőszekrény a hő természetes áramlását fordítja meg: a hideg belsejéből hőt juttat melegebb környezetébe, ami spontán módon soha nem történne meg. Ehhez külső munkavégzésre (Wbe) van szükség, amelyet általában egy kompresszor biztosít. Az energiaátvitel egyenlet szerint történik, ahol Qmeleg a környezetbe leadott hő, Qhideg pedig a hűtőből elvont hő. Bár a hűtő belsejében az entrópia csökken, a környezetébe jutó munka miatt a környezet entrópiája nagyobb mértékben növekszik. Így a teljes entrópiaváltozás (ΔSo¨sszes>0) mindig pozitív, betartva a második főtételt. Ez azt mutatja be, hogyan lehetséges lokalizált rend csak energia befektetéssel, miközben az univerzum rendezetlensége összességében mindig növekszik.
Hogyan hajlik a hang a sarkok körül:
A hang diffrakciója a hanghullámok meghajlását és széterjedését jelenti, amikor akadályokba ütköznek vagy nyílásokon haladnak át, lehetővé téve a hang számára, hogy sarkok körül terjedjen, és akkor is hallható legyen, amikor a forrás nem közvetlenül látható. Ez a jelenség annak köszönhető, hogy a hanghullámok viszonylag hosszú hullámhosszal rendelkeznek (általában 0,5–1,5 méter a hallható frekvenciák esetében), ami lehetővé teszi számukra, hogy hatékonyan diffraktálódjanak az akadályok körül. A Huygens-elv szerint a hullámfront minden pontja másodlagos hullámforrásként viselkedik, ami azt eredményezi, hogy a hullám széttart egy nyíláson való áthaladás után. Ez magyarázza, hogy az alacsonyabb frekvenciájú hangok (mint a basszus hangok vagy a motorzúgás) miért hajlanak könnyebben, mint a magasabb frekvenciájú hangok, és miért hallható valaki kiáltása egy épület sarka mögül, még mielőtt meglátnánk. A diffrakció a hullámok alapvető tulajdonsága, amely bemutatja, hogyan terjed a hangenergia és hogyan lép kölcsönhatásba a környezettel.
A zajcsillapító fejhallgatók működése – a destruktív interferencia:
A zajcsillapító fejhallgatók úgy működnek, hogy beépített mikrofonokkal észlelik a környezeti hanghullámokat. Egy processzor ezután ellenhangot generál, amely a bejövő zaj inverz (180°-os fáziseltolású) mása. Amikor ezek a hullámok találkoznak, destruktív interferencia lép fel: a környezeti hullám hullámhegyei az ellenhang hullámvölgyeivel esnek egybe, így kiolvassák egymást. Az eredmény csönd ott, ahol korábban zaj volt. E fizikai elv alkalmazásával a fejhallgatók hatékonyan csökkentik a környezeti zajokat a hallgató számára.
A Gitárhúr Harmonikusok Fizikája:
A gitárhúrok zenés hangokat állóhullámok segítségével hoznak létre, amelyek a pengetéskor keletkeznek. Ezek a hullámok meghatározott frekvenciákon, úgynevezett harmonikusokon rezegnek, melyek a húr hosszától, feszességétől és tömegsűrűségétől függenek. A húr különböző érintőinek lenyomásával a rezgő húr hossza csökken, ami megnöveli a frekvenciát és magasabb hangmagasságot eredményez. Az alapfrekvenciának (nyílt húr) a leghosszabb a hullámhossza (λ = 2L), míg a harmonikusok egész számú többszörösein (2f₀, 3f₀ stb.) jelennek meg, megkülönböztethető zenei hangzást alkotva. Ez a jelenszemény azt mutatja be, hogyan alakítják az állóhullámok és a hullámok interferenciája a hangzást a húros hangszerekben.